Suppose that $4 million is available for investment in three
projects. The probability distribution of the net present value earned from
each project depends on how much is invested in each project. Let It be the
random variable denoting the net present value earned by project t. The
distribution of It depends on the amount of money invested in project t, as
shown in Table (a zero investment in a project always earns a zero NPV).
By using forward computational procedure then solution of dynamic programming as below:
Stage: 1, 2, and 3 stand for project 1, project 2, and project 3;
Decision Variable: number of investmenst for stage i (di);
State Variable: number of initial investment at beginning of project (Si).
Stage 1:
if invest $0 and money left $4 then NPV = 0
if invest $1 and money left $3 then NPV = ($2.0x0.6)+($4.0x0.3)+($5.0x0.1)=$2.9
if invest $2 and money left $2 then NPV = (4.0x0.5)+(6.0x0.3)+(8.0x0.2)=5.4
if invest $3 and money left $1 then NPV = (6.0x0.4)+(7.0x0.5)+(10.0x0.1)=6.9
if invest $4and money left $0 then NPV = (7.0x0.2)+(9.0x0.4)+(10.0x0.4)=9.
Stage 2:
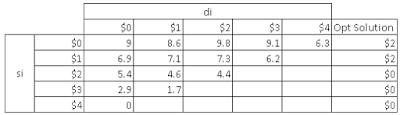
if invest $0 at stage 2
money left $4 then NPV = 0
money left $3, because used to invest $1 at stage 1 then NPV = 2.9
money left $2, because used to invest $2 at stage 1 then NPV =5.4
money left $1, because used to invest $3 at stage 1 then NPV = 6.9
money left $0, because used to invest $4 at stage 1 then NPV =9
if invest $1 at stage 2
money left $3, because used to invest $0 in stage 1 then NPV =0 + (1.0x0.5)+(2.0x0.4)+(4.0x0.1)=1.7
money left $2, because used to invest $1 in stage 1 then NPV =2.9 + (1.0x0.5)+(2.0x0.4)+(4.0x0.1)=4.6
money left $1, because used to invest $2 in stage 1 then NPV =5.4 + (1.0x0.5)+(2.0x0.4)+(4.0x0.1)=7.1
money left $0, because used to invest $3 in stage 1 then NPV =6.9 + (1.0x0.5)+(2.0x0.4)+(4.0x0.1)=8.6
if invest $2 at stage 2
money left $2, because used to invest $0 in stage 1 then NPV =0 + (3.0x0.4)+(5.0x0.4)+(6.0x0.2)=4.4
money left $1, because used to invest $1 in stage 1 then NPV =2.9 + (3.0x0.4)+(5.0x0.4)+(6.0x0.2)=7.3
Stage 1:
if invest $0 and money left $4 then NPV = 0
if invest $1 and money left $3 then NPV = ($2.0x0.6)+($4.0x0.3)+($5.0x0.1)=$2.9
if invest $2 and money left $2 then NPV = (4.0x0.5)+(6.0x0.3)+(8.0x0.2)=5.4
if invest $3 and money left $1 then NPV = (6.0x0.4)+(7.0x0.5)+(10.0x0.1)=6.9
if invest $4and money left $0 then NPV = (7.0x0.2)+(9.0x0.4)+(10.0x0.4)=9.
Stage 2:
if invest $0 at stage 2
money left $4 then NPV = 0
money left $3, because used to invest $1 at stage 1 then NPV = 2.9
money left $2, because used to invest $2 at stage 1 then NPV =5.4
money left $1, because used to invest $3 at stage 1 then NPV = 6.9
money left $0, because used to invest $4 at stage 1 then NPV =9
if invest $1 at stage 2
money left $3, because used to invest $0 in stage 1 then NPV =0 + (1.0x0.5)+(2.0x0.4)+(4.0x0.1)=1.7
money left $2, because used to invest $1 in stage 1 then NPV =2.9 + (1.0x0.5)+(2.0x0.4)+(4.0x0.1)=4.6
money left $1, because used to invest $2 in stage 1 then NPV =5.4 + (1.0x0.5)+(2.0x0.4)+(4.0x0.1)=7.1
money left $0, because used to invest $3 in stage 1 then NPV =6.9 + (1.0x0.5)+(2.0x0.4)+(4.0x0.1)=8.6
if invest $2 at stage 2
money left $2, because used to invest $0 in stage 1 then NPV =0 + (3.0x0.4)+(5.0x0.4)+(6.0x0.2)=4.4
money left $1, because used to invest $1 in stage 1 then NPV =2.9 + (3.0x0.4)+(5.0x0.4)+(6.0x0.2)=7.3
money left $0, because used to invest $2 in stage 1 then NPV =5.4 + (3.0x0.4)+(5.0x0.4)+(6.0x0.2)=9.8
if invest $3 at stage 2
money left $1, because used to invest $0 in stage 1 then NPV =0 + (4.0x0.3)+(6.0x0.3)+(8.0x0.4)=6.2
money left $0, because used to invest $1 in stage 1 then NPV =2.9 + (4.0x0.3)+(6.0x0.3)+(8.0x0.4)=9.1
if invest $4 at stage 2
money left $0, because used to invest $0 in stage 1 then NPV =0 + (3.0x0.4)+(8.0x0.3)+(9.0x0.3)=6.3
Stage 3:
if invest $0, NPV= Opt solution at stage 2 when si = $0 then = 0+9.8=9.8
if invest $1, NPV= Opt solution at stage 2 when si = $1 then = 7.3+(0.0x0.2)+(4.0x0.6)+(5.0x0.2)=10.7
if invest $2, NPV= Opt solution at stage 2 when si = $2 then = 5.4+(4.0x0.4)+(6.0x0.4)+(7.0x0.2)=10.8
if invest $3, NPV= Opt solution at stage 2 when si = $3 then = 2.9+(5.0x0.3)+(7.0x0.4)+(8.0x0.3)=9.6
if invest $4, NPV= (6.0x0.1)+(8.0x0.5)+(9.0x0.4)=8.2
Solution:
find max NPV at stage 3 then we invest $2 at stage 3, after that find max NPV at stage 2 when si=$2 then we invest $0 at stage 2, after that at stage 1 money left $2 then we invest $2 at stage 1.
if invest $3 at stage 2
money left $1, because used to invest $0 in stage 1 then NPV =0 + (4.0x0.3)+(6.0x0.3)+(8.0x0.4)=6.2
money left $0, because used to invest $1 in stage 1 then NPV =2.9 + (4.0x0.3)+(6.0x0.3)+(8.0x0.4)=9.1
if invest $4 at stage 2
money left $0, because used to invest $0 in stage 1 then NPV =0 + (3.0x0.4)+(8.0x0.3)+(9.0x0.3)=6.3
Stage 3:
if invest $0, NPV= Opt solution at stage 2 when si = $0 then = 0+9.8=9.8
if invest $1, NPV= Opt solution at stage 2 when si = $1 then = 7.3+(0.0x0.2)+(4.0x0.6)+(5.0x0.2)=10.7
if invest $2, NPV= Opt solution at stage 2 when si = $2 then = 5.4+(4.0x0.4)+(6.0x0.4)+(7.0x0.2)=10.8
if invest $3, NPV= Opt solution at stage 2 when si = $3 then = 2.9+(5.0x0.3)+(7.0x0.4)+(8.0x0.3)=9.6
if invest $4, NPV= (6.0x0.1)+(8.0x0.5)+(9.0x0.4)=8.2
Solution:
find max NPV at stage 3 then we invest $2 at stage 3, after that find max NPV at stage 2 when si=$2 then we invest $0 at stage 2, after that at stage 1 money left $2 then we invest $2 at stage 1.





Terima kasih mas,dah lama saya cari solusi untuk soal ini.
ReplyDelete